9594. ABA

Задана строка символов. Сколько раз встречается подпоследовательность “ABA” в ней? При этом буквы “ABA” могут быть не соседними, но их порядок должен сохраняться.

Вход. Одна строка, содержащая только заглавные латинские символы. Длина строки не превышает 10⁶ символов.

Выход. Выведите количество подпоследовательностей “ABA” в строке.

Пример входа 1	Пример выхода 1
YARBRBAQ	2
Пример входа 2	Пример выхода 2
ABAYBATATBBAZA	29

РЕШЕНИЕ

комбинаторика

Анализ алгоритма

Пусть s₀s₁…s_n-1 – входная строка. Пусть l[i] содержит количество букв А с позиции 0 до i-ой включительно. Пусть cnt равно общему количеству букв А в слове. Тогда справа от позиции i находится cnt – l[i] букв А.

Если буква B находится в i-ой позиции, то слева от нее находится l[i] букв А, а справа (cnt – l[i]) букв А. Количество подпоследовательностей “ABA”, где буква B находится в i-ой позиции, равно l[i] * (cnt – l[i]).

Остается просуммировать значения l[i] * (cnt – l[i]) по всем позициям i, где находится буква B.

Второе решение. Пройдем по строке слева направо и будем в переменной а подсчитывать количество букв A.

Для каждой буквы B в строке у нас образуется а слов AB (перед текущей буквой B имеется в точности а букв A). В переменной ab будем подсчитывать количество слов AB, которые встретились. Для каждой буквы B к ab следует прибавить а.

Для каждой текущей буквы A перед ней имеется ab слов AB. В переменной aba подсчитываем количество слов ABA, которые встретились. Для каждой буквы A к aba следует прибавить аb.

Пример

Рассмотрим второй тест.

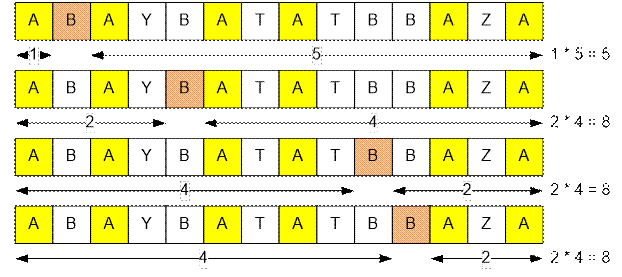
Количество подпоследовательностей “ABA” равно

1 * 5 + 2 * 4 + 2 * 4 + 2 * 4 = 5 + 8 + 8 + 8 = 29

Рассмотрим значения переменных в случае решения задачи вторым способом.

Реализация алгоритма

Читаем входную строку s.

cin >> s;

Инициализируем переменные.

cnt = 0; len = s.size();

l.resize(len);

Для каждой позиции i занесем в l[i] количество букв А с позиции 0 до i-ой включительно. По окончании цикла переменная cnt содержит общее количество букв А.

for (i = 0; i < len; i++)

{

if (s[i] == 'A') cnt++;

l[i] = cnt;

}

В переменной res подсчитываем ответ.

res = 0;

Для каждой позиции i, где находится буква В, подсчитываем количество подпоследовательностей “ABA”.

for (i = 0; i < len; i++)

if (s[i] == 'B') res += 1LL * l[i] * (cnt - l[i]);

Выводим ответ.

cout << res;

Реализация алгоритма – комбинаторный подсчет

Читаем входную строку s.

cin >> s;

Инициализируем переменные.

a = ab = aba = 0;

Перебираем символы строки. Пересчитываем переменные a, ab и aba.

for (i = 0; i < s.size(); i++)

if (s[i] == 'A')

{

a++;

aba += ab;

}

else

if (s[i] == 'B') ab += a;

Выводим ответ.

cout << aba << endl;

Python реализация

Читаем входную строку s.

s = input()

Инициализируем переменные.

cnt = 0

n = len(s)

l = [0] * n

Для каждой позиции i занесем в l[i] количество букв А с позиции 0 до i-ой включительно. По окончании цикла переменная cnt содержит общее количество букв А.

for i in range(n):

if s[i] == 'A':

cnt += 1

l[i] = cnt

В переменной res подсчитываем ответ.

res = 0

Для каждой позиции i, где находится буква В, подсчитываем количество подпоследовательностей “ABA”.

for i in range(n):

if s[i] == 'B':

res += l[i] * (cnt - l[i])

Выводим ответ.

print(res)

Python реализация – комбинаторный подсчет

Читаем входную строку s.

s = input()

Инициализируем переменные.

a = ab = aba = 0

Перебираем символы строки. Пересчитываем переменные a, ab и aba.

for c in s:

if c == 'A':

a += 1

aba += ab

if c == 'B':

ab += a

Выводим ответ.

print(aba)